Un triángulo rectángulo consta de un ángulo de 90oy dos ángulos agudos. Cada ángulo agudo de un triángulo rectángulo tiene las funciones de seno, coseno y tangente. El seno, el coseno y la tangente de un ángulo agudo de un triángulo rectángulo son rezones de dos de los tres catetos de un triángulo rectángulo.
El seno de un ángulo es la razón entre el largo del cateto opuesto del ángulo dividido por el largo de la hipotenusa.
El coseno de un ángulo es la razón entre el largo del cateto adyacente al ángulo dividido por el largo de la hipotenusa.
La tangente de un ángulo es la razón entre el largo del cateto opuesto del ángulo dividido por el largo del lado adyacente del ángulo.
Triángulo rectángulo
Antes de concentrarnos en las funciones, nos ayudará dar nombres a los lados de un triángulo rectángulo, de esta manera:
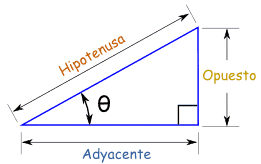
Seno, coseno y tangente
Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente. Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son!
Para el ángulo θ :
Para el ángulo θ :
Función seno:
| sin(θ) = Opuesto / Hipotenusa |
Función coseno:
| cos(θ) = Adyacente / Hipotenusa |
Función tangente:
| tan(θ) = Opuesto / Adyacente |
Nota: el seno se suele denotar sin() (por la palabra inglesa "sine") o sen(). Aquí utilizaremos sin() pero puedes encontrarte la otra notación en otros libros o sitios web.
Sohcahtoa
Sohcatoa. Es una manera de recordar qué lados se dividen! Así:
Soh...
|
Seno = Opuesto / Hipotenusa
|
...cah...
|
Coseno = Adyacente / Hipotenusa
|
...toa
|
Tangente = Opuesto / Adyacente
|
Funciones menos comunes
Para completar el cuadro, hay otras 3 funciones donde divides un lado por otro, pero no se usan tanto.
Son iguales a 1 divivido entre las tres funciones básicas (sin, cos y tan), así:
Función secante:
| sec(θ) = Hipotenusa / Adyacente | (=1/cos) |
Función cosecante:
| csc(θ) = Hipotenusa / Opuesto | (=1/sin) |
Función cotangente:
| cot(θ) = Adyacente / Opuesto | (=1/tan) |
Ejemplos
Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ?
El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado opuesto de longitud 1 y lado adyacente de longitud √3:
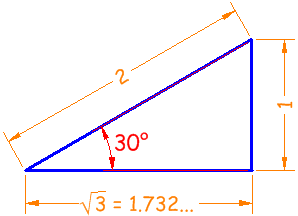
Seno
|
sin(30°) = 1 / 2 = 0.5
|
Coseno
|
cos(30°) = 1.732 / 2 = 0.866
|
Tangente
|
tan(30°) = 1 / 1.732 = 0.577
|
Ejemplo 2: ¿cuáles son el seno, coseno y tangente de 45°?
El triángulo clásico de 45° tiene dos lados de 1 e hipotenusa √2:
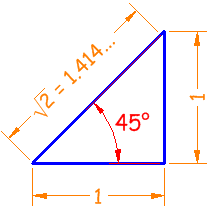
Seno
|
sin(45°) = 1 / 1.414 = 0.707
|
Coseno
|
cos(45°) = 1 / 1.414 = 0.707
|
Tangente
|
tan(45°) = 1 / 1 = 1
|






0 comentarios:
Publicar un comentario