TEOREMA DE TALES

Tales de Mileto.

   Teorema de Tales (o Thales) , hay dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente ( triángulos semejantes son los que tienen iguales ángulos ).

Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa ).

Primer teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

ó, cuando en un triangulo se traza una recta paralela a uno de los lados, el triangulo que se forma es semejante al primero.

    Dado el triángulo ABC , si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C' , cuyos lados son proporcionales a los del triángulo ABC .

 

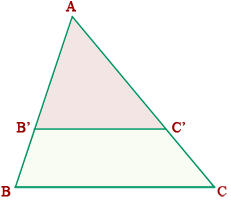
Lo que se traduce en la fórmula

Ejemplo:

 Las rectas a, b y c son paralelas. Halla la longitud de x.

Enseguida veamos un vídeo de la aplicación del Teorema de Tales